In einigen Lehrmitteln kommt es gelegentlich vor, dass bei einem Rechendreieck nur mit Hilfe der Aussenzahlen die Innenzahlen herausgefunden werden müssen. Die Aufgabe kann evtl. durch Ausprobieren gelöst werden, es gibt jedoch eine elegantere Möglichkeit, welche hier vorgestellt wird:
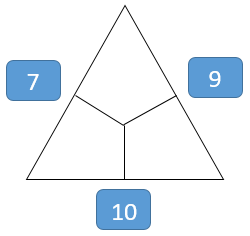
- Aussenzahlen addieren: 9 + 10 + 7 = 26
- Ergebnis halbieren: 26 : 2 = 13
- Ergebnis minus kleinste Aussenzahl: 13 – 7 = 6
- Ergebnis im Dreieck gegenüber der kleinsten Aussenzahl eintragen.
Die nun noch fehlenden Innenzahlen können wie üblich ausgerechnet werden.

Rosemary meint
Brilliant! Danke!
Diego meint
Oder weiter machen:
13-9= 4
13-10= 3
MoSH meint
Lösung: rechts = (b + c – a)/2
oben + links = a
oben + rechts = b
links + rechts = c
oben = a – links
oben = b – rechts
links = c – rechts
a – links = b – rechts
a – (c- rechts) = b – rechts
rechts = (b + c – a)/2
Bei a=7, b=9, c=10 ergibt das rechts = (9 + 10 – 7)/2 = 6
birgit meint
Super erklärt…Danke
Dennoch suche ich nach einer einfachen Erklärung für Schüler der 1. Klasse
Katharina Plass meint
Ich meine, dass dieser Rechenweg zu kompliziert ist für Grundschüler, vor allem ist er nicht leicht zu verstehen – diese Methode “funktioniert” einfach, ohne dass man weiß, warum.
Wir haben einen einfacheren Weg gefunden, der auch gut mit Figuren oder Klötzchen veranschaulicht werden kann:
Auf der rechten Seite ist die Zahl um 2 größer als auf der linken Seite, also müssen auch in der rechten unteren Ecke 2 mehr sein als in der linken, da in der oberen Ecke die Zahl ja für beide Seiten gleich ist.
Von der unteren Zahl wird 2 abgezogen, die später die rechte Ecke bekommt. Der Rest 8 wird zwischen den beiden unteren Ecken aufgeteilt, jede Ecke bekommt 4, und die rechte Ecke bekommt noch die 2 dazu, die vorher abgezogen wurde.
3 5 und 7 meint
Wie kann ich ein Rechendreieck lösen mit den Zahlen 3 5 und 7?
Idris meint
Ist die Summe der Außenzahlen ungerade lassen sich Rechendreiecke nicht mit ganzen Zahlen lösen, da die Summe d. Innenzahl = 1/2 der Summe d. Außenzahlen sind.